Predictive collision detection techniques

In preparation for my upcoming Flash game programming training courses, I’m getting my head back into game physics, and I so I thought I’d share some useful collision detection methods I’ve discovered over the last few years.

Reactive collision detection

Collision detection in Flash games often occurs after things have moved. So you have a circle (usually a 2D representation of a ball) and you’re moving it towards a vertical line on the side of the screen (representing a wall). Every frame, you update its position and check whether it’s overlapping the wall.

Which is great, but of course if the ball is moving fast it may go from one side of the wall all the way to the other side between frames and no collision is detected. One way to get around this is to split up the movement of the ball into small segments and run this check several times between frames. This seems pretty inelegant to me so I have always strived to use predictive collision detection methods where my maths knowledge has allowed me! (This is also known as sweep testing, frame independent or continuous collision detection (CCD)).

Predicting when things will collide before you move them

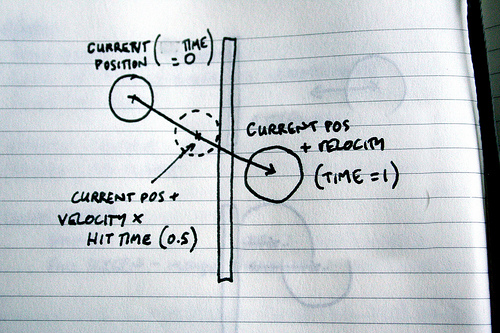
So rather than just check whether the ball is intersecting with the wall between renders, we actually check the velocity of the ball to see at what point in time it would hit the wall if it continued in the direction it’s going.

If the ball is moving at 10 pixels per frame and the wall is 30 pixels away then we know that we will hit it in 3 frames. And if the wall is 15 pixels away we know that we will hit it at some point between the next frame and the frame after.

But if it’s 5 pixels away then we know that the ball will hit the wall exactly half way between the last frame and the next. And more importantly we know that the collision occurred after the ball had moved half of its velocity. So not only do we know when the collision occurred, we also can work out where the ball is when it collided.

So imagine this code is running between frames :

 

// the distance from the wall to the ball
distance = wallX-(ballX+radius); 

// timeHit is the time that the ball will hit the wall in frames: 0 is now, 
// 1 is the next frame, 2 is the frame after that
timeHit = distance / velX; 

// if timeHit is between 0 and 1 we know that the ball will hit the wall 
// within this update
if((timeHit>0) && (timeHit<1))
{
   // we have a collision! As the hit time is between 0 and 1 we can 
   // multiply the velocity by that number to find the collision point
   ballX += (velX*timeHit); 
   ballY += (velY*timeHit); 

   // at this point we would do a collision reaction, here's a simple 
   // bounce assuming the ball is on the left and the wall is on the right
   velX *= -1; 
}

Moving the ball to its collision point

The really great thing about this method is that you genuinely find out where the collision happened as opposed to discovering an intersection and then trying to work out how to move your objects back to stop them overlapping.

Of course this is a very basic example, and it may be that simpler methods would suffice in this case. But as we get into more complex examples you’ll see exactly how valuable this technique can be.

Coming next – predicting collisions between circles.