In my previous collision detection post, I talked about predicting whether two objects would collide in between frames. This is to avoid the situation where the objects are moving so fast that they pass through each other before you’ve had a chance to see if they’re overlapping. This is often known as a sweep test (amongst other things!)
And I showed how you could predict collisions between a 2D circle and a vertical line but what about lines that aren’t vertical? How do you work out collisions between circles and lines of any angle?
Here is where vector maths comes in, so if you haven’t looked at it since school, here’s a great article that will tell you the basics (based around Processing but you’ll get the jist). And for further study you can look at this very comprehensive guide from the CCSU.
So we have our circle flying around and we want to test whether it’s colliding with the line, in other words are they overlapping? Logic dictates that if the distance from the line to the centre of the circle is less than the circle’s radius then it must be penetrating (stop giggling at the back!). But how do we find this distance?
When I started solving these sort of problems I’d use trigonometry: right angled triangles and sine cosine and tan. But I later learned that you can use some magic vector maths to do the same thing much much faster. But first there are some things you need to know about :
Dot product
The dot product of 2 vectors is a number that varies depending on the angle between them. It’s called the dot product because it’s sometimes represented with a ‘˙’ symbol. It’s calculated by multiplying the various elements of the two vectors together. Use this interactive demo to see how the dot product changes as you move the vectors around.
[kml_flashembed publishmethod=”dynamic” fversion=”9.0.0″ movie=”/wp-content/uploads/manual/2010/physicstutorials/DotProduct.swf” width=”560″ height=”400″ targetclass=”flashmovie”]
[/kml_flashembed]
In particular, notice how the dot product is negative when the angle between the vectors is greater than 90º and positive when the angle is less than 90º. Also note that the dot product is 0 when the vectors are perpendicular to each other. This will be very useful to us later on.
Normals
Simply put, a normal is a vector that is at a right angle to a line, and it’s usually a unit vector, ie a vector that is 1 unit long.
Shortest distance between a line and a circle
Let’s say we have a line defined by two points P1 and P2, the line normal is N, and our circle’s centre point is C. We also have the vector between P1 and C, called (rather unimaginatively) P1C.
To find out the distance between C and the line you simply get the dot product between P1C and N. So if this distance is less than the radius of the circle then we know we’ve got an overlap and therefore the circle is colliding with the line!
You can see it here in this example, click to drag the points and the circle around.
[kml_flashembed publish method=”dynamic” fversion=”9.0.0″ movie=”/wp-content/uploads/manual/2010/physicstutorials/PointLineDistance.swf” width=”560″ height=”400″ targetclass=”flashmovie”][kml_flashembed]
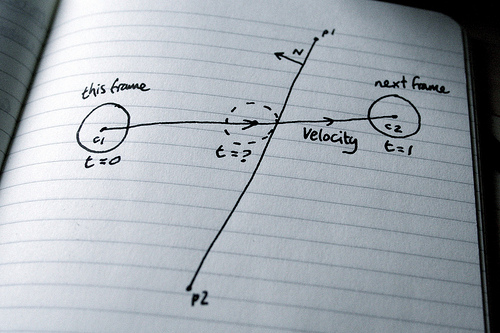
Predicting collisions between a circle and a line
So you know the distance between the line and where the circle is now (lets call it d1), and what the distance will be in the next frame (d2), but what we need to know is how far along were we between frames when (and if) there will be a collision. A collision occurs when the distance is equal to the radius, and we’re trying to find a value for t (time) where t = 0 now and t = 1 in the next frame.
We can use this formula :
current distance = d1 + (d2-d1) * t
so when d = the radius r :
r = d1 + (d2-d1) * t
and with some algebra even I can just about manage we can extract t :
r-d1 = (d2-d1)*t (r - d1) / (d2-d1) = t
So if t is between 0 and 1 we know we collided between frames!
Whew. This blog post is getting epic. But we’re not quite there yet, we still need to work out where the circle is at the point of collision: we take the vector between C1 and C2, multiply it by t and add it to C1.
Here’s an example that shows this all in action :
[kml_flashembed publishmethod=”dynamic” fversion=”9.0.0″ movie=”/wp-content/uploads/manual/2010/physicstutorials/CircleLinePredictive.swf” width=”560″ height=”400″ targetclass=”flashmovie”][/kml_flashembed]
I’ll continue this series further to explain :
- collision reactions
- collisions between moving circles
- and all the same for 3D – spheres and planes!
I really hope this is useful, it’s actually really hard to explain this in writing, so let me know if any of it is unclear. And of course I’ll be explaining this in more detail in my game programming training courses.

35 replies on “Predicting circle line collisions”
OMG, this is so useful! thanks!
I’ve always had an awful time working with vectors, specially cause I never really understood the operations involved, for instance, why a dot product is just a number (and not another vector) and what does it represents in “cartesian” terms? ^^… Those links about vectors seem great.
A dot product is just a single number (or a scalar) because it’s the product of the various elements of the vectors added together. As the vectors are described in values along each axis (x,y) they’re known as cartesian. This is as opposed to vectors in polar format (a length and a rotation).
Im still planning to implement this technique in AS3, but my Math isnt good enough (yet): //www.metanetsoftware.com/technique/tutorialA.html
(i have no idea if it’s better/worse/different then what you’re doing, but
“Separating Axis Theorem” sounds impressive right?
I’ve used SAT before – it’s a great technique, I think it’s safe to say it’s more commonly used for intersection tests between polygons. I’m not sure if you can do a sweep test with that method?
Is this technique more efficient than doing a coordinate rotation?
Are there any other differences between the two techniques?
I haven’t done any benchmarking but I this method would definitely be faster than any rotational methods, at least if the line’s normal is precalculated (calculating a normal requires a processor-intensive square root). Dot products are very quick to calculate, if we have two vectors (x1,y1) and (x2,y2) the formula is :
so it’s very quick!
Sorry I didn’t get back to you on the last post. This is great. Those explorations are really clear.
Before I was talking about testing for point collision with a bounding box by taking the dot product of the motion vector and each axis then comparing them to the axis-oriented sides of the bounding box.
I like the direction you’re going with the circle bounding a lot, though.
I implement this kind of collisions predicting in my papervision 3d tour.. to create camera slide effect along the wall..
//dreamflashstudio.com/my_lab/my3dTour/
Yes of course, this method is perfect for the “slide” effect (and it works in 3D but more about that later!). Are you doing collisions with every triangle? Great demo!
no, I didn’t do for every triangle, I just create a invisible plane object along the wall. that’s all. The challenge is papervision detect a hit for a plane abject as a cube. So I use this method to do “really” plane detection. And add extra calculation to make sure camera far little bit from wall to avoid clipping issues in 3D
Something wrong with the first example, the simple dot-product one.
If you use two vectors of length 1, the resulting dot product should be inside the range -1 to 1, but I can get it all the way to 20.
I think you’re working in pixels instead of grid units or something.
Great tutorial otherwise 🙂
that’s weird, I fixed that ages ago! I guess it’s version control issues. Fixed again now! 🙂
Gee, this is a lot simpler than my method I was using! But there’s still something wrong…
What happens when the ball hits the tip of a line segment? You assume that the line goes on forever, but this is rarely the case in games. If the ball hit the tip of a line segment, the distance between the ball center and the normal line would be less than the radius of the circle, and the distance between the ball center and the tip would have to equal the radius of the circle. I don’t know how to do that
Um, I was thinking about the problem for a bit; I might have come up with a solution:
First, do the circle-line collision normally. Then find, if the circle collides with the line, the point on the line closest to the center of the circle. If this point isn’t between the 2 corners of the line segment, ignore the collision.
Second, do a circle-circle collision with the two corners of the segment, and assume the corners are circles with radii of 0
yes, that’s exactly it, check the endpoints as circles. Good luck!
I’d be curious to see what Seb’s take is on cases where where d1 < r, that is when the circle (C1) already intersects the line. As implemented, Seb's app reports no collision when d1 < r and maybe he has good reason to want it that way. For me, though, it makes it hard to adapt this particular circle-line method to handle collisions between circles and finite line segment. It also throws and wrench into a line-segment solution proposed by a comment above: "First, do the circle-line collision normally …" because while your circle may not be already colliding with a finite line segment, it may well be already colliding with an infinite line and you'd be none the wiser.
Update on circle line-segment collisions: The following solution seems to work for me, and I think it should be faster than what has been proposed so far in this forum for line segments. The basic idea is to split line-segment collisions into two mutually-exclusive cases (endpoint collisions vs. line collision) based on the particular arrangement of (p1,p2) and (c1,c2) vectors.
To decide on which of the two cases applies, compute the point on the (p1,p2) line that’s closest to c1 and call that point e1. The (c1,e1) vector has length d1 in Seb’s demo. Then check if the length of the (c1,e1) vector is < r. If it is, then line collision is irrelevant and all you need to worry about are the segment's two endpoints (see link below on how to handle circle-circle collisions in a predictive way). If it is not, then simply apply Seb's method for line collision.
I can see two benefits to splitting line-segment collisions into two mutually-exclusive cases. First, it should be fast because it computes solutions either for the endpoint cases or for the line case but never both. Second, it handles cases where the circle might already be intersecting with the infinity line even if the circle doesn't intersect with the finite line segment (notice how Seb's method doesn't flag a collision if the circle already intersects the line).
Another thing to bear in mind is that Seb's method only handles positive collisions (i.e., Seb expects d1 to be positive). If you want to handle two-sided line collisions, then compute d1 and d2 as you normally would, but if d1 is negative then multiply d1 and d2 by (-1) before computing t. Flipping the signs of d1 and d2 is equivalent to recomputing d1 and d2 with the line's opposite normal but should be computationally faster.
Hope this helps.
//ericleong.me/research/circle-circle
In your demo the ball allways hits the left side of the wall…
even if you switch the C points…
That’s wrong.
How can you determine which side of the wall the ball hit?
Maybe switch d1 and d2 if you detect (Using dot product) that it’s pointing against the wall normal.??
btw:Do you have a code/lib with this functionality? I can give it a good use 😉
Thanks
Gil
Great tutorial Seb, I really like ur style.
@Gil : I’m a little late but to answer your post, you can get the normals from the line pointing to each C point, no matter which side it’s on. A line in 2-space has 2 normals, they are both determinable given a point on either side (ie the positions of C1 & C2). Here’s my (c#) code to get the normals :
Vector2 displacement = pointPos – ClosestPointOnLineToPoint(pointPos, lineP1, lineP2);
displacement.Normalize();
The normalized displacement vector between the wall and the given circle is
the surface normal for that circle.
this is a very nice tutorial you’ve got here. one of the most comprehensive i’ve seen – there are a few small problems though. for instance, i don’t know how you missed this, but, in your last example, when the circle is overlapping the line at c1 no collision is detected. also, since the normal is always pointing to the same side of the line, your collision equation only works when the normal if facing c1. there’s probably an easier way to fix this, but you could write a function that determines which side of the line c1 is on, returning -1 for left and 1 for right, then multiply the normal by that result. otherwise, nice work – it really helped me understand dot product a lot better.
excellent tutorial. I was able to figure out a problem I had with my ball line collision. I looked all over the net but found no valid solution until I came across this post. I learned most of what I know from Tonypa website. It’s a really good beginner website to learn from, if you at least know basic structures.
now because of this thread I got most of what I want to learn figured out. The engine has ball to static circle collision, ball to static arc collision(from inside and outside), ball to line collision(works perfect due to your tutorial here), and moving ball to moving ball collision. all working with friction and gravity.
the only problem I have now is that I want to create a pinball game and the only thing I am missing is how to collided against a rotating flipper. I have done it somewhat accurately by rotating the vector line(flipper) one pixel at a time and test until point of collision but that is not as efficient as it should be,it’s rather slow. I have been cracking my head trying to figure it out using different methods and reading on tutorials but no luck.
would you be able to explain in a tutorial? or can you supplying the necessary formulas(equations) for the solution? or maybe post some links to tutorials or usable info?
If you have a mac and want to see what I have so far you can download a demo from here: //www.mediafire.com/?6y46uly0rqoshnw
If forgot to mention that what I really need is the time of collision between t=0 and t=1
Hello good post but I am stuck!
How do you calculate the normal from two points?
Point a = x:0,y:0
Point b = x:0,y = 100
(representing a straight line, the left side of my screen)…
|————
|
|
|
|————-
I tried cross product:
vector = b-a
cross = x:-vector.y,y:vector.x
But im just confusing myself 🙁
@James
components:
vx = b.x-a.x
vy = b.y-a.y
length = Sqrt(vx*vx+vy*vy)
normal:
dx = vx/length
dy = vy/length
left normal:
lx = dy
ly = -dx
right norma:
rx = -dy
ry = dx
what you need is the left Normal
Awesome awesome! Exactly what I was looking for! Thank you Seb!
[…] has written a few interesting articles about Predictive collision detection techniques and Predicting circle line collisions which i highly recomend a read. At first Vector math blew my mind but with some time I have been […]
Thanks a lot for this.
Nitpicks: Could mention at least that d1 and d2 in your final equation are signed. I assumed they were standard distance measurements (which aren’t signed) and so spent half an hour trying every combination of the math to figure out what was going on.
I then guessed that d1 and d2 could have a sign based on whether the circle made it through to the other side – and then everything worked.
This is also really ambiguous: “so when d = the radius r :” What is “d”? I just ignored this comment and found the rest of it easier to follow.
Actually, fuck it – here’s a function that does the tutorial above:
package com.nitrome.geom {
import flash.geom.Point;
/**
* Returns the value to multiply vx and vy to resolve collision
*
* Inferred circle-line swept collision from
*
* //seblee.me/2010/01/predicting-circle-line-collisions/
*
* @author Aaron Steed, nitrome.com
*/
public function circleLineSweep(circle:Circle, line:Line, vx:Number, vy:Number):Number{
var toCircleX:Number, toCircleY:Number;
toCircleX = circle.x – line.a.x;
toCircleY = circle.y – line.a.y;
var lineDistStart:Number = toCircleX * line.rx + toCircleY * line.ry;
toCircleX = (circle.x + vx) – line.a.x;
toCircleY = (circle.y + vy) – line.a.y;
var lineDistEnd:Number = toCircleX * line.rx + toCircleY * line.ry;
// the circle’s path and the line are parallel
if(lineDistEnd – lineDistStart == 0) return Number.NaN;
return (circle.radius – lineDistStart) / (lineDistEnd – lineDistStart);
}
}
I’ll leave it to the reader to write their own line and circle objects. line.rx is the right hand normal of the line. Getting the distance by multiplying by the normal gives a signed distance, letting you know what side of the line you’re on.
As said above t >= 0 && t <= 0 is a collision.
What if p2 is (0,0), p1 is (0,-1), c1 is (-5,0), and c2 is (5,0)
basically if the normal is pointing towards c2
Great post! I have one issue though. Are you sure about the formula for t being (r – d1) / (d2-d1)? Look at this situation:
r = 12;
d1 = -15;
d2 = -8;
This is a collision, and t should be between 0 and 1.
(12–15)/(-8–15) = 27/7 = 3.85, which signifies a collision in 3 frames.
Am I missing something here?
This code is a single sided collision, which means that it predicts a collision on the positive side. It’ll take 3 frames to get from the negative side to be on the edge of the positive side, so you’ll need to adjust the algorithm for a negative-side collision. Hope this helps!
I am STRUGGLING to understand the shortest distance example. Is there any way that you would be willing to share the .FLA or .AS on this one? Specifically, I get the Dot Product, but have zero idea how you are getting the normal vector. I understand its the inverse of the p1 / p2 vector, but am under sure how it relates to your comment about getting it down to 1 unit. Any help would be super appreciated!
Hey Scott,
it’s such an old post I’m not sure where the code is! To get the normal you need the perpendicular of P1->P2 and then normalise it to get the unit vector.
To get the perpendicular : //mathworld.wolfram.com/PerpendicularVector.html
To normalise a vector, get the length of the vector and divide both x and y components by that length.
Hope this helps!
Seb
Thanks Seb!
It is an old post indeed, but still super relevant! While searching for the answer, I kept coming back to this post. Meaning that your organization and presentation are perfect.
Thanks for the direction!