Super fast triangle/rectangle intersection test

I’m always on the lookout for ways to speed up our project work and also some of the inner workings of Papervision3D, and I must admit, sometimes it reaches fairly obsessive levels, bordering on unhealthy. In fact sometimes the minor optimisations are so insignificant, it can just be an exercise in problem solving. Which let’s face it, we all do from time to time just for fun, right? 😉

The latest target for my attention is the triangle / rectangle intersection check that happens just before rendering. It’s way after any of the clever 3D stuff, we’re just literally looking at whether the 2D triangle we’re about to draw is within the rectangle that represents our screen.

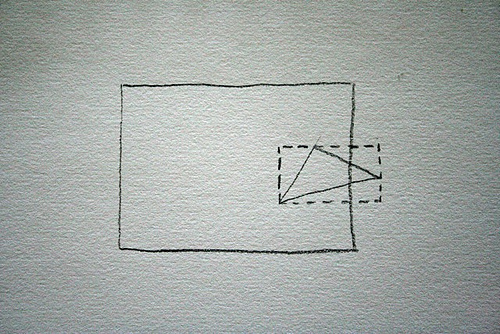
The current check is a simple bounding rectangle check. The bounding rectangle for the triangle is calculated and we use a simple intersect check for the two rectangles. Which is simple and fast. But it was bothering me that huge offscreen triangles were not getting culled because their bounding rectangle overlapped with the viewport rectangle.

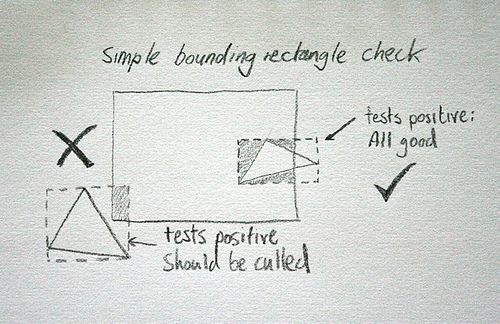
So how do you accurately check that a triangle is intersecting a rectangle? Here’s one way :

1) Check if any of the triangle’s points are within the rectangle, if yes then intersection is true.
2) Check if any of the triangle’s lines intersect any of the rectangle’s lines, if yes then intersection is true.

Check 1 is relatively simple, but if no points are within the rectangle, we have to move to check 2, and that means we have to check each of the 3 lines in the triangle with each of the 4 lines of the rectangle, 12 line intersection checks altogether. Which just felt a bit dirty to me.

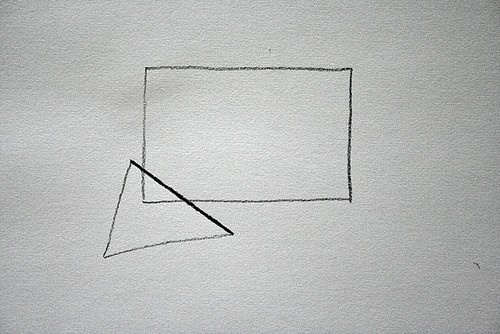
But then I got to thinking, this rectangle is an AABB (or axis-aligned bounding box, which basically means that it’s not rotated), so that should make things a little easier. And I developed this little technique loosely based on existing systems but I haven’t seen anything exactly like this before. I’m not sure if it’s the best way but it seems fast and accurate to me! Here’s how it works :

1) take the first line of the triangle

2) calculate its equation and then work out the y position that it intersects the left and right edges of the rectangle

3) take the maximum and minimum y bounds of those two intersection points and calculate the overlap between those and the max and min y values of the line.

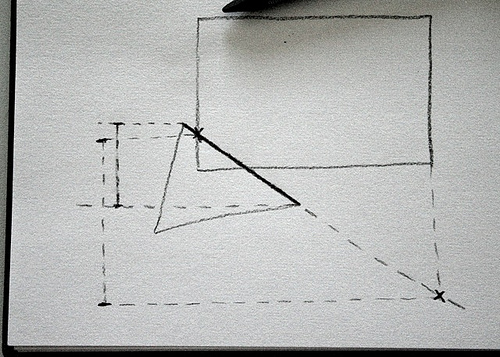
4) if these new overlapping min and max y values overlap the top and bottom of the rectangle then the line (and therefore the triangle) must intersect the rectangle, so return true.

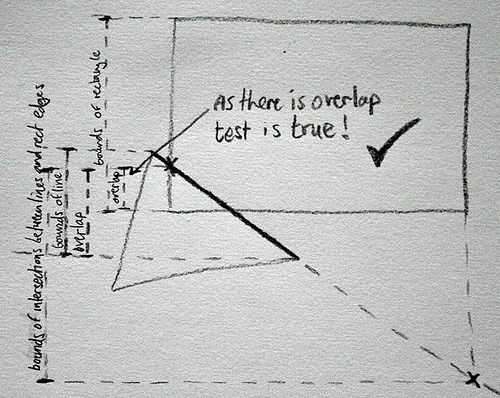
5) Otherwise move on to the next line of the triangle and try again.

It seems to be much more accurate than the existing bounding rectangle check and for positives is 30% faster. For negatives it’s about the same or a tiny bit slower. The only innaccuracy I’ve found is if the triangle is entirely containing the rectangle it returns negative. And also I should put in a check for vertical lines and do a simpler check on those.

But my challenge to you! Can you get this to be slicker / faster? I’m sure there are some maths wizards out there. Full code below and you can even fork it and have a play at the rather awesome Wonderfl

I realise that you could unroll the method call to triangleAABBIntersectionTest but I’m more interested in improvements to the maths/logic.

Good luck!

package
{
   import flash.display.Graphics;
   import flash.display.Sprite;
   import flash.events.MouseEvent;
   import flash.geom.Point;
   import flash.geom.Rectangle;
   import flash.text.TextField;
   import flash.text.TextFormat;
   import flash.utils.getTimer;
   [SWF(frameRate="100", backgroundColor="0x000000", width="500", height="500")]

   public class TriangleAABBSpeedTest extends Sprite
   {


      public var outputText : TextField;

      public function TriangleAABBSpeedTest()
      {
         super();
         outputText = new TextField();
         x = y = 250;
         outputText.defaultTextFormat = new TextFormat("Arial");
         outputText.textColor = 0xffffff;
         outputText.text = "Click to start test";
         outputText.x = outputText.y = -250;
         outputText.width = 500;

         addChild(outputText);

         stage.addEventListener(MouseEvent.MOUSE_DOWN, startTest);

      }

      // I'm thinking that storing these values as properties rather than declaring them as local vars
      // should be faster...

      private  var x0 : Number;
      private  var y0 : Number;
      private  var x1 : Number;
      private  var y1 : Number;
      private  var x2 : Number;
      private  var y2 : Number;
      private  var l : Number;
      private  var r : Number;
      private  var t : Number;
      private  var b : Number;

      private  var top_intersection:Number ;
      private  var bottom_intersection : Number;
      private  var toptrianglepoint : Number;
      private  var bottomtrianglepoint : Number;

      private  var m: Number;
      private var c : Number


      // THESE ARE THE TWO FUNCTIONS YOU CAN OPTIMISE.
      // I realise that you could inline the lineRectangleIntersect method, but I'd rather not do that just yet...
      // I'm looking for maths/logic improvements.

      public function triangleAABBIntersectionTest(rect:Rectangle,  vertex0:Point, vertex1:Point, vertex2:Point ) : Boolean
      {
         // YOU MUST LEAVE THESE DECLARATIONS; they simulate necessary data exchange within PV3D
         l = rect.left;
         r = rect.right;
         t = rect.top;
         b = rect.bottom;

         x0 = vertex0.x;
         y0 = vertex0.y;
         x1 = vertex1.x;
         y1 = vertex1.y;
         x2 = vertex2.x;
         y2 = vertex2.y;


         return lineRectangleIntersect(x0,y0,x1,y1)
               ||   lineRectangleIntersect(x1,y1,x2,y2)
               ||   lineRectangleIntersect(x2,y2,x0,y0);



      }


      public function lineRectangleIntersect(x0: Number,y0: Number,x1: Number,y1: Number):Boolean //, left:Number, right:Number, top:Number, bottom:Number) : Boolean
      {

            // Calculate m and c for the equation for the line (y = mx+c)
            m = (y1-y0) / (x1-x0);
            c = y0 -(m*x0);

            // if the line is going up from right to left then the top intersect point is on the left
            if(m>0)
            {
               top_intersection = (m*l  + c);
               bottom_intersection = (m*r  + c);
            }
            // otherwise it's on the right
            else
            {
               top_intersection = (m*r  + c);
               bottom_intersection = (m*l  + c);
            }

            // work out the top and bottom extents for the triangle
            if(y0toptrianglepoint ? top_intersection : toptrianglepoint;
            botoverlap = bottom_intersection<bottomtrianglepoint ? bottom_intersection : bottomtrianglepoint;

            // (topoverlap<botoverlap) :
            // if the intersection isn't the right way up then we have no overlap

            // (!((botoverlapb)) :
            // If the bottom overlap is higher than the top of the rectangle or the top overlap is
            // lower than the bottom of the rectangle we don't have intersection. So return the negative
            // of that. Much faster than checking each of the points is within the bounds of the rectangle.
            return (topoverlap<botoverlap) && (!((botoverlapb)));

      }











      public function startTest(e:MouseEvent = null) : void
      {
         var g : Graphics = graphics;
         g.clear();
         var cullingRect : Rectangle = new Rectangle(-100,-75,200,150);

         var iterations : int = 100000;
         var timerIntersecting : int = 0 ;
         var timerNotIntersecting : int = 0 ;
                        var intersectCount : int = 0;

         var v0 : Point = new Point();
         var v1 : Point = new Point();
         var v2 : Point = new Point();

         var i : int = iterations;

         while(--i>-1)
         {
            v0.x = Math.random()*400 - 200;
            v0.y = Math.random()*400 - 200;
            v1.x = v0.x+ (Math.random()*300 -150);
            v1.y = v0.y+ (Math.random()*300 -150);
            v2.x = v0.x+ (Math.random()*300 -150);
            v2.y = v0.y+ (Math.random()*300 -150);

            var startTimer : int = getTimer();
            var intersecting : Boolean = triangleAABBIntersectionTest(cullingRect, v0, v1, v2);
            if(intersecting)
            {
               timerIntersecting += (getTimer() - startTimer);
               intersectCount++;
            }
            else
            {
               timerNotIntersecting += (getTimer() - startTimer);
            }
            if(i<300)
            {
               g.lineStyle(0,0x000000);
               g.beginFill(intersecting ? 0x006600 : 0x660000,0.5);
               g.moveTo(x0,y0);
               g.lineTo(x1,y1);
               g.lineTo(x2,y2);
               g.lineTo(x0,y0);
               g.endFill();
            }
         }

         g.lineStyle(0,0xffffff,0.5);
         g.drawRect(cullingRect.x, cullingRect.y, cullingRect.width, cullingRect.height);
         outputText.text = "Average time per triangle : "+(timerIntersecting+timerNotIntersecting)/iterations;
         outputText.appendText("nAverage time per intersecting triangle : "+(timerIntersecting)/intersectCount);
         outputText.appendText("nAverage time per non-intersecting triangle : "+(timerNotIntersecting)/(iterations-intersectCount));

      }

   }
}